bzoj 1001 [BeiJing2006]狼抓兔子 题解

发表于 | 分类于 | | 热度: ℃

Description

给定一 $n*m$ 的网格图。每条边有一个流量，兔子从左上角 $(1,1)$ 跑到右下角 $(n,m)$。流量为 $k$ 的边需要 $k$ 匹狼才能堵住。

求把兔子一网打尽所需的最少的狼。

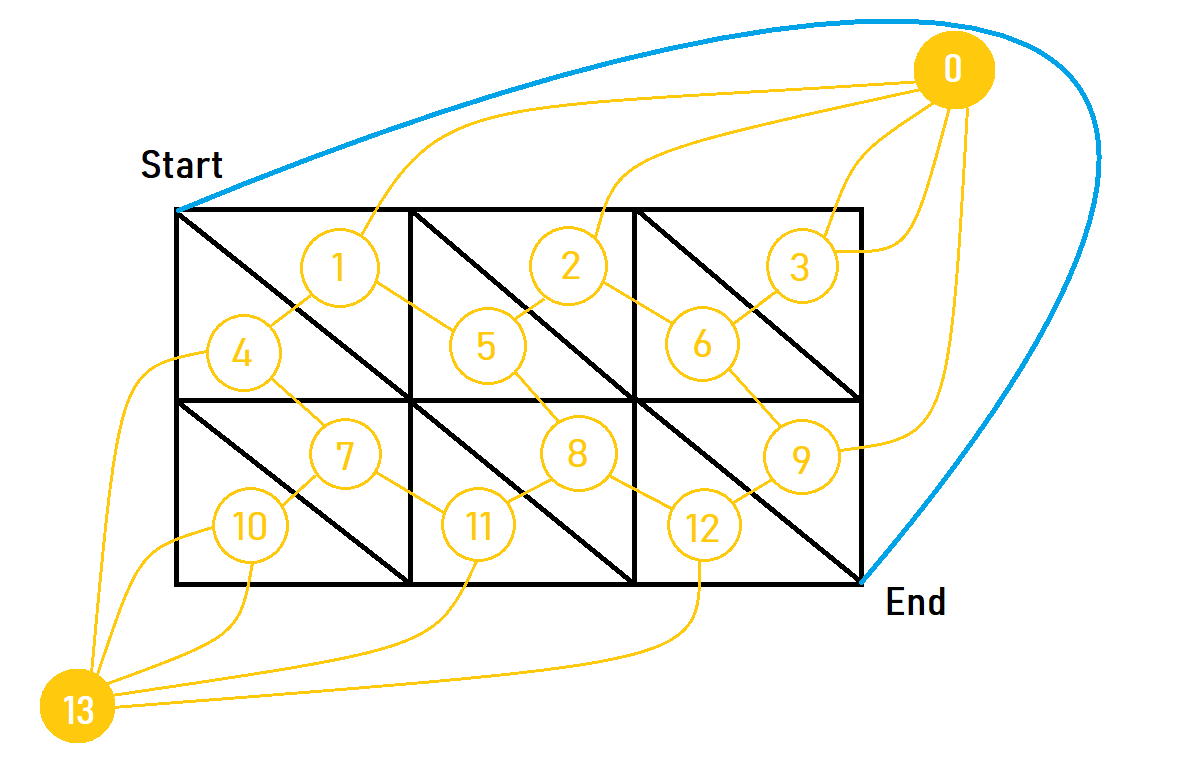
如图：

数据范围：$n,m<=1000$

Solution

首先想到的是最大流 $=$ 最小割，可以跑一遍网络流。$TLE$。还有一个定理：平面图的最大流 $=$ 其对偶图的最短路。建对偶图，然后跑 $dijkstra+$ 堆优化。

平面图

一边只在顶点处相交的图（其边不存在交叉）

对偶图

定义

对于每一个平面图， 都有与其相对应的对偶图。假设上面的例图是 $G$，与其对应的对偶图为 $G’$,那么对于 $G’$ 上面的每一个点， 对应的是 $G$ 里面的每一个面。

构建方式

如图。对于每条边，用一条 垂直于 它的边连接对应的两个点（面）

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#define M (n - 1) * (m - 1) * 2 + 1
using namespace std;

const int N = 1000006;
struct edge
{
    int nxt, to,w;
} e[N * 6 + 106];
struct node
{
    int id, dis;
    friend bool operator < (node x, node y)
    {
        return x.dis > y.dis;
    }
};
priority_queue < node > q;
int n, m, a, cnt = 0, dis[N * 2 + 106], vis[N * 2 + 106], head[N * 2 + 106];

inline int read()
{
    char c = getchar(); int x = 0, f = 1;
    while(c < '0' || c > '9') { if(c == '-') f = -1; c = getchar(); }
    while(c >= '0' && c <= '9') { x = x * 10 + c - 48; c = getchar(); }
    return x * f;
}

void add(int x, int y, int w)
{
    e[++cnt] = (edge) { head[x], y, w };
    head[x] = cnt;
    e[++cnt] = (edge) { head[y], x, w };
    head[y] = cnt;
}

void dijkstra()
{
    memset(dis, 0x3f, sizeof(dis));
    memset(vis, 0, sizeof(vis));
    q.push((node) { 0, 0 });
    dis[0] = 0;
    while(!q.empty())
    {
        int a = q.top().id;
        q.pop();
        if(vis[a]) continue;
        vis[a] = 1;
        for(int i = head[a]; i; i = e[i].nxt)
        {
            int v = e[i].to;
            if(dis[v] > dis[a] + e[i].w)
            {
                dis[v] = dis[a] + e[i].w;
                if(!vis[v])
                    q.push((node) { v, dis[v] });
            }
        }
    }
}

int ID(int x, int y, int k)
{
    if(k == 1) return (x - 1) * (m - 1) * 2 + y;
    return (x - 1) * (m - 1) * 2 + y + m - 1;
}

int main()
{
    n = read(), m = read();
    memset(head, 0, sizeof(head));
    if(n == 1 || m == 1)
    {
        int f = 0x3f3f3f3f;
        for(int i = 1; i < max(n, m); i++)
        {
            a = read();
            f = min(f, a);
        }
        printf("%d", f);
        return 0;
    }
    for(int i = 1; i <= n; i++)
        for(int j = 1; j < m; j++)
        {
            a = read();
            if(i == 1) add(ID(i, j, 1), 0, a);
            else if(i == n) add(ID(i - 1, j, 2), M, a);
            else add(ID(i, j, 1), ID(i - 1, j, 2), a);
        }
    for(int i = 1; i < n; i++)
        for(int j = 1; j <= m; j++)
        {
            a = read();
            if(j == 1) add(ID(i, j, 2), M, a);
            else if(j == m) add(ID(i, j - 1, 1), 0, a);
            else add(ID(i, j, 2), ID(i, j - 1, 1), a);
        }
    for(int i = 1; i < n; i++)
        for(int j = 1; j < m; j++)
        {
            a = read();
            add(ID(i, j, 1), ID(i, j, 2), a);
        }
    dijkstra();
    printf("%d", dis[M]);
    return 0;
}